Gerak dengan Analisis Vektor

Gerak dengan Analisis Vektor

Jika kita belajar fisika maka kita akan sering mempelajari tentang gerak. Fenomena tentang gerak memang sangat menarik. Coba perhatikan tentang gerak pada gambar di samping. Dari gambar itu saja dapat timbul banyak pertanyaan yang perlu dijawab. Bagaimana kecepatan awal anak tersebut, bagaimana posisi tiap saatnya, bagaimana agar jangkauannya jauh. Ada juga pertanyaan apakah jenis-jenis gerak yang dapat kita amati? Semua hal itu dapat kita jawab dengan mempelajari bab ini. 

 

Oleh sebab itu setelah belajar bab ini diharapkan dapat:
1. menentukan perpindahan, kecepatan dan percepatan sebuah benda yang bergerak secara vektor,
2. menentukan kecepatan sudut, percepatan sudut dan percepatan linier pada benda yang bergerak melingkar,
3. menentukan kecepatan sudut, percepatan sudut dan percepatan linier pada benda yang bergerak parabola.

Posisi, Kecepatan Dan Percepatan Pada Gerak Dalam Bidang

Gerak Lurus yang dipelajari di Kelas X dapat dianalisis tanpa menggunakan vector.

Tetapi gerak pada bidang (dua dimensi) maka kita harus menganalisisnya dengan menggunakan vector. Secara umum, besaran gerak (Posisi, Kecepatan dan Percepatan) diuraikan atas dua komponen yang saling tegak lurus.

Ø  POSISI r = x i +  y j m

pada benda yang memiliki koordinat ( x , y)

Contoh :

Sebuah partikel berada pada koordinat (3,2) meter, maka penulisan persamaan posisinya adalah

r = x i +  y j m

r = 3 i +  2 j   m

Ø  KECEPATAN v = v_x i + v_y j m/s

pada benda yang memiliki kecepatan ( v_x , v_y)

Contoh :

Sebuah partikel bergerak dengan kecepatan (4,1) m/s, maka penulisan persamaan kecepatannya adalah

v = v_x i + v_y j m/s

v = 4 i +     j m/s

Ø PERCEPATAN a = a_x i + a_y j m/s²

pada benda yang memiliki kecepatan ( a_x , a_y)

Contoh :

Sebuah partikel bergerak dengan percepatan(5,3) m/s², maka penulisan persamaan percepatannya adalah

a = a_x i + a_y j m/s²

a = 5 i +  3  j m/s²

Bagaimana bila partikel berpindah posisi dari titik P(3,2)m menuju ke titik Q(5,5)m ?

Perpindahan adalah perubahan posisi/kedudukan suatu partikel dalam selang waktu tertentu dimana titik awal P dan titik akhir Q

Maka perpindahan partikel memenuhi persamaan :

Δr = r_Q – r_P

Δr = (x₁i + y₁j) – (x₂i + y₂j)  meter

Δr = (x₂i – x₁i) + (y₂j – y₁j)  meter

atau Δr = Δx i  + Δy j

sehingga

Δr = (5i + 5j) – (3i + 2j) meter

Δr = (5i – 3i) + (5j – 2j) meter

Δr =  2i +  3j meter

Berapa besar perpindahannya ?

Δr² = (2i)² +  (3j)² meter

Δr² = 4.i² +  9.j² meter karena  i² = 1 dan j² = 1 maka

Δr² = 4  +  9

Δr = (4  +  9)^½ atau √ 13

Penggunaan Operasi Integral Dan Diferensial/Turunan

Posisi (r), Kecepatan (v) dan percepatan (a) dengan penyelesaian matematis menggunakan diferensial/turunan dan integral bisa didapatkan bila salah satu variable diketahui persamaannya.
Lihat Diagram berikut !

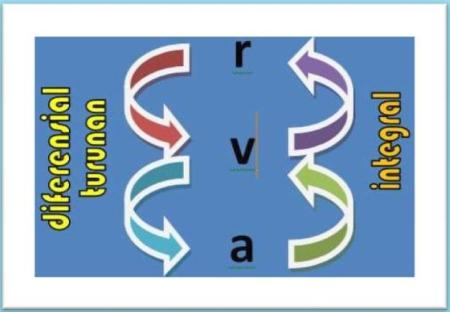
• Bila r diketahui, maka v dan a dapat dicari dengan diferensial/turunan, demikian juga bila v diketahui a didapat dari penurunan v
• Bila diketahui, maka persamaan kecepatan (v) dan posisi (r) dapat ditentukan dengan integral, demikian pula bila v diketahui, posisi dapat diselesaikan.

RUMUS DIFERENSIAL DAN INTEGRAL

DIFERENSIAL/TURUNAN
Bila posisi
r =  tⁿ
maka persamaan kecepatan
v = dr/dt
v = d(tⁿ)/dt
v =  n.t^n-1
Demikian pula bila, kecepatan
v =  2tⁿ
maka persamaan percepatan
a = dv/dt
a = d(2.tn)/dt
a =  2.nt^n-1


INTEGRAL
Bila percepatan
a  =  tⁿ
maka persamaan kecepatan
v = ∫ a dt
v = ∫ tⁿ dt
v = (1/(n+1))x t ⁿ⁺¹ + c